20 de março de 2018 | Anf. 3.2.14 | 17:00

“George Pólya e a resolução de problemas em Matemática”
Henrique Guimarães (Instituto de Educação – ULisboa)
“A Matemática não é um desporto para espectadores: não a podemos apreciar, nem aprender, sem uma participação activa.” (Pólya, 1967)
Resumo:
George Pólya (1887-1985) é um matemático húngaro, nascido em Budapeste, cidade onde realizou todos os seus estudos até se doutorar em Matemática em 1912, com um estudo sobre probabilidade geométrica.

Pólya foi um matemático muito fecundo em domínios matemáticos muitos diversos, com uma grande produção individual e em colaboração com outros matemáticos de renome que conheceu e com quem conviveu, ainda durante os seus estudos de pós-graduação, e depois em Zurique para onde se mudou em 1914. Foi nesta cidade, onde ingressou no Instituto Federal de Tecnologia da Suíça, que desenvolveu grande parte do seu trabalho científico e que encontrou grandes matemáticos da altura. Aqui viveu até que, por altura da segunda guerra, em 1940, se mudou para os Estados Unidos da América instalando-se em Palo Alto, na Califórnia, como professor na Universidade de Stanford, onde permaneceu até ao fim da sua vida.
George Pólya desenvolveu uma parte importante do seu trabalho igualmente em domínios não estritamente ligados à investigação científica que desde muito cedo o interessaram. Em 1945 publica aquele que viria a ser o seu ‘best-seller’ traduzido em inúmeras línguas e ainda hoje em distribuição — How To Solve It. Na tradução portuguesa recebeu o título “Como resolver problemas”, e é o primeiro livro que dedica por inteiro às suas ideias sobre a resolução de problemas e a heurística ou ‘o estudo dos métodos e das regras da invenção e da descoberta’ em matemática.
É justamente com base neste livro, e recorrendo a alguns exemplos e outros livros onde Pólya desenvolveu e aprofundou as suas ideias sobre os temas que mencionei, que irei procurar evidenciar alguns dos traços principais do seu pensamento sobre a actividade matemática e, em particular, sobre a resolução de problemas.

“[Um professor] de Matemática, se desafia a curiosidade dos seus alunos, apresentando-lhes problemas adequados aos seus conhecimentos e ajudando-os com interpelações estimulantes, poderá despertar neles o gosto pelo pensamento independente e proporcionar-lhes alguns meios para o concretizarem.” (Pólya, 1945)

 dificuldades que se ergueriam perante iniciativas de o racionalizar. É neste contexto que no início do século 20, David Hilbert, classifica o problema da clarificação do Infinito, como um dos mais importantes problemas aguardando uma solução. Esta conferência pretende ilustrar estas dificuldades e dar conta de “progressos” matemáticos no sentido da sua clarificação.
dificuldades que se ergueriam perante iniciativas de o racionalizar. É neste contexto que no início do século 20, David Hilbert, classifica o problema da clarificação do Infinito, como um dos mais importantes problemas aguardando uma solução. Esta conferência pretende ilustrar estas dificuldades e dar conta de “progressos” matemáticos no sentido da sua clarificação.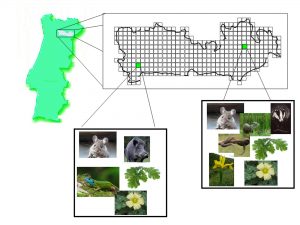 tem por objetivo produzir conhecimentos e estabelecer procedimentos que possam contribuir para a persistência da diversidade biológica. A definição de áreas prioritárias para a conservação da biodiversidade é um tópico importante em Biologia da Conservação. Vamos ver que a Matemática está intimamente ligada ao estudo deste tópico.
tem por objetivo produzir conhecimentos e estabelecer procedimentos que possam contribuir para a persistência da diversidade biológica. A definição de áreas prioritárias para a conservação da biodiversidade é um tópico importante em Biologia da Conservação. Vamos ver que a Matemática está intimamente ligada ao estudo deste tópico.


 or vezes, surpreendentes.
or vezes, surpreendentes. RESUMO: O cálculo numérico acompanha desde sempre a matemática e as suas aplicações. Ao longo dos últimos séculos cresceu muito a utilização do cálculo numérico, apoiada na evolução de máquinas e métodos cada vem mais rápidos e sofisticados.
RESUMO: O cálculo numérico acompanha desde sempre a matemática e as suas aplicações. Ao longo dos últimos séculos cresceu muito a utilização do cálculo numérico, apoiada na evolução de máquinas e métodos cada vem mais rápidos e sofisticados.